QUANTIFYING AMMI MODEL IN TERMS OF GENETIC PARAMETERS

L. P. Subedi

IAAS/Tribhuvan University, Rampur, Chitwan, Nepal

E-mail:<kiran@scn.mos.com.np>

ABSTRACT

Genotype-by-environment interaction (GEI) is a measure of differential response of genotypes to varied environmental conditions. Its effects are to limit the accuracy of yield estimation from multienvironmental evaluation of varietal performance. There are various models developed by different workers to predict the GEI. I have developed two models: variable active genic (VAG) and variable active parental genic proportions (VAPGeP) model. There are other models like AMMI (additive main effects and multiplicative interactions), that are extensively used these days. Non genetic parameters like eigen value and eigen vectors as well as principal components are computed in the latter model to predict GEI. In this presentation, I have equated different genetic parameters of the genetic model (my model) to eigen value, vectors and principal components and have provided their genetic meaning. For these purpose different populations: purelines and composites were computer generated. In general, the following relationship was established.

(GxE)_ij=(`A_i.-`A..)(a_j-`a.)+(D_i.-`D..)(d_j-`d.) +.. (In terms of genetic model = VAG model)

=±l₁v_1iu_1j±l₂v_2iu_2j±.. (in terms of AMMI model) = Y_ij -`Y_i.-`Y._j +`Y..

Where A_i= difference between number of homozygous dominant and homozygous recessive loci of i^th genotype D_i= Number of heterozygous loci of i^th genotype; a_j=additive genetic effect for j^th environment d_j=dominant effect for j^th environment l_m=square root of m^th eigen value v_mi and u_mj are corresponding genotypic and environmental eigen vectors.Y_ij refers to the yield of i^th genotype in j^th environment. The variances of distribution generating a_j’s and d_j’s were significantly correlated with eigen values, and A_i and D_i effects were highly correlated with genotypic eigen vectors. Similarly, a_j and d_j effects were found highly correlated with environmental eigen vectors. However, the AMMI model was found mechanical as compared to the VAG model. Moreover, active genetic constitution can also be computed by simulating ANOVA and predicting genetic parameters.

KEYWORD: purelines, composites, eigen value, eigen vector, genetic constitution

INTRODUCTION

Evaluation of genotypic performance in multi environment trials is the main activity in any plant-breeding program. Understanding and predicting of crop response to environment is very important. It is an outcome of the research work in physiology, agronomy, modeling and, genetics and plant breeding. Better understanding of adaptation leads to more efficient and targeted crop improvement strategy. Level of adaptation is a function of the genotype or the genetic constitution and its response to the environment it occupies. In other words, it is the function of the genes possessed by the plants and their regulation during growth and development. Therefore, the genotype-by-environment interaction (GEI), which is the differential response of genotypes to the varied environmental conditions, results from the genetic differences among varieties and their resulting influence on growth and development. This differential response is also a function of individual as well as population buffering. Whatever is the cause of GEI, a significant GEI complicates the selection of superior and widely adapted genotype thus encouraging biodiversity while a low level of GEI enhances the selection of widely adapted genotype resulting the reduced biodiversity.

MATERIALS AND METHODS

The materials and methods basically consist of description and computer application of two models: i) variable active genic (VAG) model and ii)additive main effects and multiplicative interactions (AMMI) model.

VARIABLE ACTIVE GENIC (VAG) MODEL

The VAG model assumes the genetic dynamism of active genetic constitution, where some basic loci and some other variable loci control the character of interest and the species under consideration is diploid with 2 alleles per locus. The additive, dominance and interaction components of genetic mean are also assumed to vary from one level of environment to other. Under this assumption, the phenotypic value (Y_ijt) of i ^th (I= 1,2,….,n) entry at j^th (j=1,2,…..,p) environment in t^th (t= 1,2,…,.r) replication within environment, can be represented as (Subedi, 1996):

Where:
m
_{w jt}=
the average of the phenotypic values of homozygous dominant and homozygous recessive genotypes of w^th locus at j^th environment and t^th replication within jth environment.

K_ijt = the number of active loci i^th entry at j^th environment and t^threplication within j^th environment. The numbers of active loci vary among entries or genotypes because of hypostatic relation (interaction) among some genes.

P_iwuv= the frequency of A_vA_u genotype at w^th locus in the i^th entry.

Following relation holds good for different populations:

Purelines: P_iwu=0 or 1; P_iwuv= 0 if u¹v
Mixtures: 0£Piwu ³ 1; P_iwuv= 0 if u ¹ v
Hybrids: P_iwu= 0 or 0.5 or 1; P_iwuv = 0 or 1 if u ¹ v
Synthetic:P²_iwu = P_iwuu; 2P_iwu P_iwv = P_iwuv and P²_iwv = P_iwvv
In all cases, P_iwu +P_iwv = 1.0

a_wjt= the mean of the difference between the phenotypic values of homozygous dominant and homozygous recessive genotype of w^th locus at j^th environment and t^th replication within j^th environment . a_wjt is zero for all inactive loci. A hypostatic gene (allele) is considered inactive.

d_wjt= the difference between the phenotype values of a heterozygous genotype of w^th locus and its corresponding m_wjt at the j^th environment and t^th replication within the j^th environment.

q_wi = 1, 0, -1 for homogygous dominant, heterozygote and homozygous recessive genotype, respectively, of w^th locus in the i^th entry.

GENERATING PERFORMANCE

Different populations: purelines and composites were generated as of Subedi (1996). The yield of a genotype is generated at two levels: a) first of all, the genotype is generated and then genetic constitution parameters (K_i, A_i , D_i) are computed based on its genetic constitution, and b) these parameters are then multiplied by m_j, a_j and d_j, respectively and added them together.

GENERATING GEI

Different magnitudes and types of GEI are basically generated by changing the variance of distributions generating a_j’s and d_j’s.

AMMI MODEL

The basic linear model used in the analysis of GEI is of the form:

Y_ij= m +g_i +Î_j + d_{ij :} Where, (GXE)_ij=d_ij g_i = genotypic effect of i^th genotype, and Î_j= environmental effect of j^th environment and m=grand mean = `Y.. In Additive Main Effects and Multiplicative Interactions (AMMI) model (Shafii et al.,1992), the yield is partitioned as:

Y_ij= m + g_i + Î_j + (l₁ v_1iu_1j + l₂ v_2iu_2j +…)

l_m is the singular value of the matrix E^TE (square root of eigen value of PCA axis m), where E is the n x p matrix of residuals (d_ij) . The v_mi and u_mj are corresponding normalized eigen vectors of matrix EE^T and E^TE , respectively. Genotype PCA score and environment PCA score are expressed as unit vector times the square root of l_m. The GEI sum of squares is divided into PCA axes where axis m is regarded as having n+p-1-2m degrees of freedom, where n and p are the number of genotypes and environments, respectively.

COMPARING THE VAG MODEL WITH THE AMMI MODEL

Different criteria are used to compare these two models. First of all, variance of distribution generating a_j’s of VAG model and l₁ ² (sum of squares explained) by first component of AMMI model were regressed to find any relationship that exits between the models. Secondly, the GEI sum of squares explained by different components of the two models was compared.

COMPUTING GENETIC ARCHITECTURE OF TEST GENOTYPES

Actual analysis of variance (ANOVA) of multi-environment tested performance of a set of genotypes is simulated and compared. If there exits a significant relationship among the different components of the two models between actual and simulated ANOVA, then these two ANOVA are declared similar. The A_i and D_i effects if found similar to either first or second PCA scores warrant a situation where an approximate genetic constitution or architecture of the tested genotypes can be computed. For the sake of example, the rapeseed data of Shafii et al. (1992) was used in this study, to illustrate this point.

RESULTS AND DISCUSSION

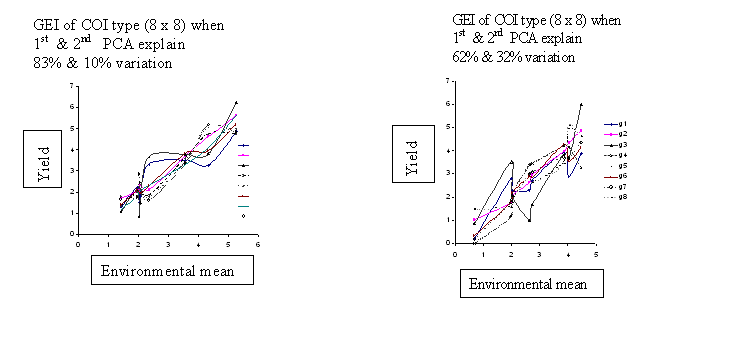
The diagrams generated through varying magnitude and types of GEI are presented in Figure 1. Diagrams indicate basically two main points: a) the number of cross-over interactions are equal to or less than minimum of (n,p):number of genotypes or number of environments , and b) most of the variations in GEI is predicted by first two PCA scores (PCA1 and PCA2).

The sum of squares of GEI predicted by different components of the VAG and the AMMI models are presented in Table 1. In some situations (first three cases), each component of both models predict almost equal magnitude of GEI, while rest of the cases, the same is not true. In the latter case also, the magnitude of GEI predicted by first two components (VAG2 vs AMMI2) are almost equal to themselves and to the magnitude of actual GEI. This indicates the existence of following relationship:

VAG2 = ±l₁v_1iu_1j ± l₂v_2iu_2j±…= Y_ij- `Y_i. - `Y._j+ `Y..

It has been found (data not presented here) that the components of AMMI model may have similar or differing signs, throughout.

The relationship between the distribution generating a_j’s and weighted eigen values (l₁²/np) is presented in Figure 2. The figure compares this relationship for two types of the populations: purelines and composites. This relationship should be viewed in the light of the last 3 sets of data in table 1. It indicates that there exists a significant relationship, although may not be 1:1, between the parameters of the two models.

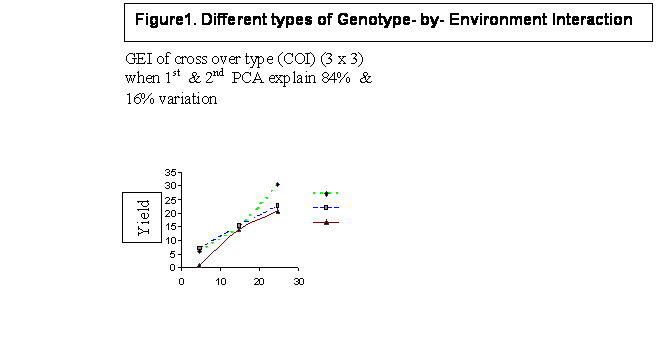
Table 1. Comparison between different components of AMMI and

VAG models for their predictability of sum of squares due to GEI

AMMI1	VAG 1	AMMI 2	VAG 2	Actual	Df (n=p)
12.33	12.77	19.27	19.76	20.38	49
19.41	19.47	31.16	30.03	37.18	49
42.61	51.68	63.1	68.1	67.0	49
11.06	1.38	13.51	12.13	12.93	4
19.89	7.75	19.76	17.86	19.91	4
11.44	0.61	12.81	11.51	12.26	4

AMMI 1 = l₁v_1iu_1j AMMI 2 = l₁v_1iu_1j + l₂v_2iu_2j

VAG 1 = (`A_i. - `A.) (a_j-`a.)
VAG 2 = (`A_i. - `A.) (a_j-`a.) + (`D_i.-`D.) (d_j -`d.)

n = no. of genotypes p = no. of environments